项目背景

企业用电需求预测一直是电力市场营销活动业务难点，大数据与云计算、人工智能等新技术相结合，给传统行业转型升级带来了新的机遇和思考。本项目主要用到开放扬中市高新区1000多家企业的历史用电量数据，通过模型算法预测该地区下一个月的每日总用电量。

数据采集

本项目主要用到开放扬中市高新区1000多家企业的历史用电量数据，直接在官网下载csv文件即可。

数据处理


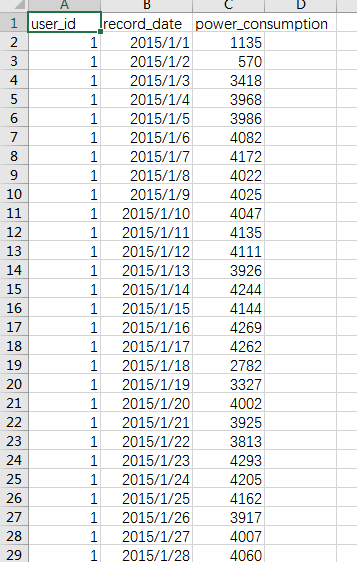
从上面的图可以看到，原始数据主要由3个维度组成：user_id,record_date,power_consumption,分别对应企业ID，日期以及用电量

日期格式转换

因为原数据的日期是strting类型，所以我们需要把它格式转换

1
2
3
4
import pandas as pd
f = open('电力数据power_AI.csv')
df = pd.read_csv(f)
df['record_date'] = pd.to_datetime(df['record_date'])

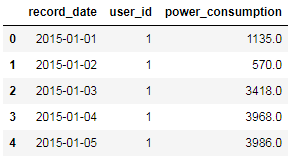
统计每日均值

1
2
3
base_df = df[['record_date','power_consumption']].groupby(by='record_date').agg('sum')
base_df = base_df.reset_index()
base_df.head()

特征工程

因为数据只有3个维度，可能会造成欠拟合的情况，所以我们利用日期构建一些特征。

增加日期特征

1
2
3
4
5
6
7
8
9
10
11
12
base_df['dow'] = base_df['record_date'].apply(lambda x: x.dayofweek)
base_df['doy'] = base_df['record_date'].apply(lambda x: x.dayofyear)
base_df['day'] = base_df['record_date'].apply(lambda x: x.day)
base_df['month'] = base_df['record_date'].apply(lambda x: x.month)
base_df['year'] = base_df['record_date'].apply(lambda x: x.year)

def map_season(month):
    month_dic = {1:1, 2:1, 3:2, 4:2, 5:3, 6:3, 7:3, 8:3, 9:3, 10:4, 11:4, 12:1}
    return month_dic[month]

base_df['season'] = base_df['month'].apply(lambda x: map_season(x))
base_df.head()

增加月度特征

1
2
3
4
5
6
7
8
base_df_stats = new_df = base_df[['power_consumption','year','month']].groupby(by=['year', 'month']).agg(['mean', 'std'])
base_df_stats.columns = base_df_stats.columns.droplevel(0)
base_df_stats = base_df_stats.reset_index()
base_df_stats['1_m_mean'] = base_df_stats['mean'].shift(1)
base_df_stats['2_m_mean'] = base_df_stats['mean'].shift(2)
base_df_stats['1_m_std'] = base_df_stats['std'].shift(1)
base_df_stats['2_m_std'] = base_df_stats['std'].shift(2)
base_df_stats.head()

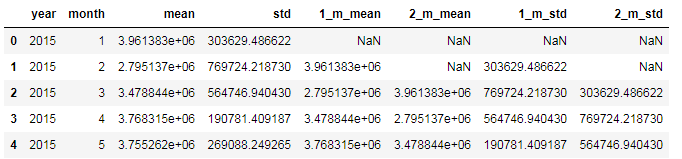
相关性检测

1
2
3
4
5
6
7
8
9
10
11
12
13
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set_style('darkgrid') #设定绘图的背景样式
sns.set_palette('muted') #设定图表的颜色板
plt.style.use('ggplot')
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
corrmat = data_df[internal_chars].corr() #计算相关系数
f , ax = plt.subplots(figsize = (10,6)) #设置图标尺寸大小
plt.xticks(rotation = '0')
sns.heatmap(corrmat, square=False, linewidths=.8, annot=True) #设置热力图参数

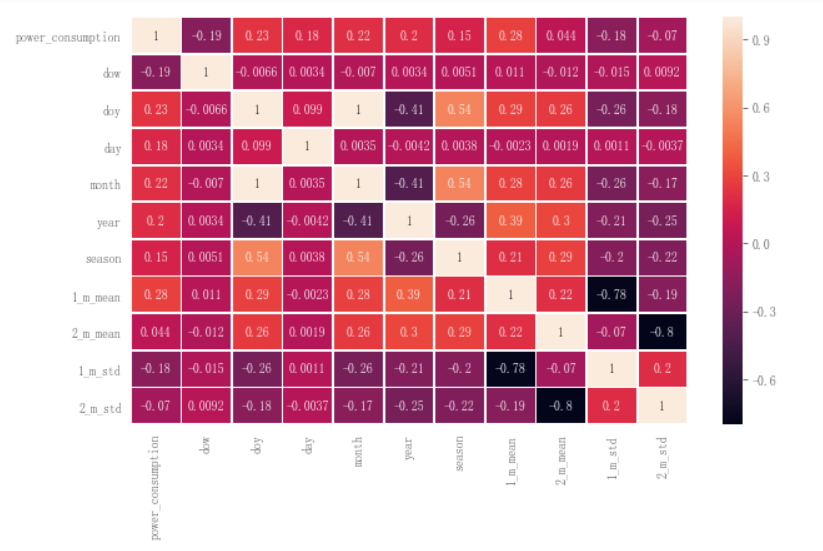
数据分析

企业与用电量的关系


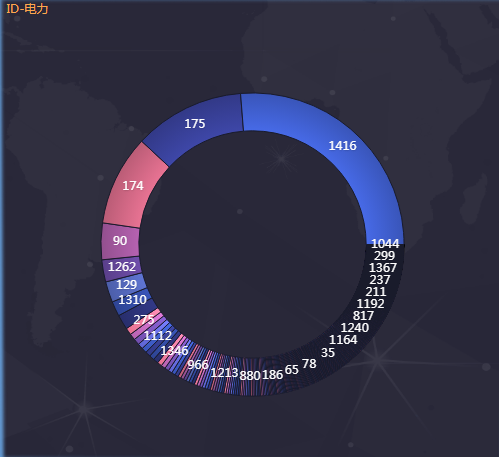
可以看到ID为1416,174,175的企业用电量很大
如果有必要可以把这3个企业单独分为1类做处理。

时间维度与用电量的关系





数据建模

在这个项目中，我们主要用到XGboost这个算法模型

训练模型

首先我们用模型默认的参数进行预测

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
df_finall = pd.read_excel('data_all.xlsx',sheet_name='V2')#加载数据
from sklearn.cross_validation import KFold, train_test_split
from xgboost import XGBRegressor
from sklearn import metrics
from sklearn.cross_validation import KFold, train_test_split
X = df_finall.iloc[:,1:-1]
X[['dow','doy','day','month','year','season']] = X[['dow','doy','day','month','year','season']]\
.astype(str)
y = df_finall.iloc[:,-1]
X_train, X_test, y_train, y_test = train_test_split(X.values, y.values, test_size=0.3)
xgb1 = XGBRegressor()
xgb1.fit(X_train,y_train)
test_predictions = xgb1.predict(X_test)
r2 = metrics.r2_score(y_test, test_predictions)
r2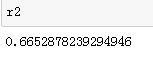

参数微调

因为XGBoost自带的参数较多，所以我们采用网格搜索的方式对参数进行微调。

  • Step 1: 选择一组初始参数
    1
    xgb1 = XGBRegressor(eta=0.01, num_boost_round=50, colsample_bytree=0.5, subsample=0.5,objective='reg:linear',seed=27)
  • Step 2: 改变 max_depth 和 min_child_weight.
    1
    2
    3
    4
    5
    xgb_param_grid = {'max_depth': list(range(4,9)), 'min_child_weight': list((1,3,6))}
    grid = GridSearchCV(XGBRegressor(eta=0.01, num_boost_round=50, colsample_bytree=0.5, subsample=0.5,objective='reg:linear',seed=27),
                    param_grid=xgb_param_grid, cv=5)
    grid.fit(X_train, y_train)
    grid.grid_scores_, grid.best_params_, grid.best_score_
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    ([mean: 0.66566, std: 0.11042, params: {'max_depth': 4, 'min_child_weight': 1},
      mean: 0.65945, std: 0.10346, params: {'max_depth': 4, 'min_child_weight': 3},
      mean: 0.65507, std: 0.08334, params: {'max_depth': 4, 'min_child_weight': 6},
      mean: 0.67838, std: 0.09230, params: {'max_depth': 5, 'min_child_weight': 1},
      mean: 0.65974, std: 0.09295, params: {'max_depth': 5, 'min_child_weight': 3},
      mean: 0.65113, std: 0.08137, params: {'max_depth': 5, 'min_child_weight': 6},
      mean: 0.68250, std: 0.08758, params: {'max_depth': 6, 'min_child_weight': 1},
      mean: 0.66546, std: 0.10096, params: {'max_depth': 6, 'min_child_weight': 3},
      mean: 0.65293, std: 0.09142, params: {'max_depth': 6, 'min_child_weight': 6},
      mean: 0.67734, std: 0.08246, params: {'max_depth': 7, 'min_child_weight': 1},
      mean: 0.66691, std: 0.09677, params: {'max_depth': 7, 'min_child_weight': 3},
      mean: 0.66142, std: 0.08414, params: {'max_depth': 7, 'min_child_weight': 6},
      mean: 0.67381, std: 0.11030, params: {'max_depth': 8, 'min_child_weight': 1},
      mean: 0.67931, std: 0.09550, params: {'max_depth': 8, 'min_child_weight': 3},
      mean: 0.66090, std: 0.08821, params: {'max_depth': 8, 'min_child_weight': 6}],
     {'max_depth': 6, 'min_child_weight': 1},
     0.6825025931707269)
    网格搜索发现的最佳结果:
    {‘max_depth’: 6, ‘min_child_weight’: 1}
  • Step 3: 调节 gamma 降低模型过拟合风险.
    1
    2
    3
    4
    5
    xgb_param_grid = {'gamma':[ 0.01 * i for i in range(0,5)]}
    grid = GridSearchCV(XGBRegressor(eta=0.01, num_boost_round=50, colsample_bytree=0.5, subsample=0.5,objective='reg:linear',seed=27,max_depth=7,min_child_weight=1),
                    param_grid=xgb_param_grid, cv=5)
    grid.fit(X_train, y_train)
    grid.grid_scores_, grid.best_params_, grid.best_score_
    1
    2
    3
    4
    5
    6
    7
    ([mean: 0.67462, std: 0.09512, params: {'gamma': 0.0},
      mean: 0.67462, std: 0.09512, params: {'gamma': 0.01},
      mean: 0.67462, std: 0.09512, params: {'gamma': 0.02},
      mean: 0.67462, std: 0.09512, params: {'gamma': 0.03},
      mean: 0.67462, std: 0.09512, params: {'gamma': 0.04}],
     {'gamma': 0.0},
     0.6746192263207629)
    网格搜索发现的最佳结果:
    {‘gamma’: 0.0}
  • Step 4: 调节 subsample 和 colsample_bytree 改变数据采样策略.
    1
    2
    3
    4
    5
    6
    7
    xgb_param_grid = {'subsample':[ 0.1 * i for i in range(6,10)],
                          'colsample_bytree':[ 0.1 * i for i in range(6,10)]}
    grid = GridSearchCV(XGBRegressor(eta=0.01, num_boost_round=50, colsample_bytree=0.5, subsample=0.5,objective='reg:linear',seed=27,max_depth=7,
                                     min_child_weight=1,gamma=0),
                    param_grid=xgb_param_grid, cv=5)
    grid.fit(X_train, y_train)
    grid.grid_scores_, grid.best_params_, grid.best_score_
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    ([mean: 0.67014, std: 0.13270, params: {'colsample_bytree': 0.6000000000000001, 'subsample': 0.6000000000000001},
      mean: 0.67302, std: 0.10802, params: {'colsample_bytree': 0.6000000000000001, 'subsample': 0.7000000000000001},
      mean: 0.66858, std: 0.11634, params: {'colsample_bytree': 0.6000000000000001, 'subsample': 0.8},
      mean: 0.67034, std: 0.11901, params: {'colsample_bytree': 0.6000000000000001, 'subsample': 0.9},
      mean: 0.66074, std: 0.12567, params: {'colsample_bytree': 0.7000000000000001, 'subsample': 0.6000000000000001},
      mean: 0.67163, std: 0.11620, params: {'colsample_bytree': 0.7000000000000001, 'subsample': 0.7000000000000001},
      mean: 0.67011, std: 0.11888, params: {'colsample_bytree': 0.7000000000000001, 'subsample': 0.8},
      mean: 0.67345, std: 0.10611, params: {'colsample_bytree': 0.7000000000000001, 'subsample': 0.9},
      mean: 0.67388, std: 0.11610, params: {'colsample_bytree': 0.8, 'subsample': 0.6000000000000001},
      mean: 0.67462, std: 0.10752, params: {'colsample_bytree': 0.8, 'subsample': 0.7000000000000001},
      mean: 0.68473, std: 0.10995, params: {'colsample_bytree': 0.8, 'subsample': 0.8},
      mean: 0.69456, std: 0.08956, params: {'colsample_bytree': 0.8, 'subsample': 0.9},
      mean: 0.66677, std: 0.11420, params: {'colsample_bytree': 0.9, 'subsample': 0.6000000000000001},
      mean: 0.66556, std: 0.10918, params: {'colsample_bytree': 0.9, 'subsample': 0.7000000000000001},
      mean: 0.67706, std: 0.11681, params: {'colsample_bytree': 0.9, 'subsample': 0.8},
      mean: 0.67529, std: 0.11429, params: {'colsample_bytree': 0.9, 'subsample': 0.9}],
     {'colsample_bytree': 0.8, 'subsample': 0.9},
     0.6945571414092301)
    网格搜索发现的最佳结果:
    {‘colsample_bytree’: 0.8, ‘subsample’: 0.9}
  • Step 5: 调节学习率 learning_rate.
    1
    2
    3
    4
    5
    xgb_param_grid = {'learning_rate':[0.6,0.5,0.4,0.3,0.2,0.1,0.01,0.001]}
    grid = GridSearchCV(XGBRegressor( num_boost_round=50,objective='reg:linear',seed=27,max_depth=7,
                                     min_child_weight=1,gamma=0,colsample_bytree=0.8,subsample=0.9),param_grid=xgb_param_grid, cv=5)
    grid.fit(X_train, y_train)
    grid.grid_scores_, grid.best_params_, grid.best_score_
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    ([mean: 0.56345, std: 0.18185, params: {'learning_rate': 0.6},
      mean: 0.60402, std: 0.16560, params: {'learning_rate': 0.5},
      mean: 0.67215, std: 0.13258, params: {'learning_rate': 0.4},
      mean: 0.63116, std: 0.13087, params: {'learning_rate': 0.3},
      mean: 0.62305, std: 0.16146, params: {'learning_rate': 0.2},
      mean: 0.69456, std: 0.08956, params: {'learning_rate': 0.1},
      mean: -12.66985, std: 4.34214, params: {'learning_rate': 0.01},
      mean: -77.40167, std: 26.16110, params: {'learning_rate': 0.001}],
     {'learning_rate': 0.1},
     0.6945571414092301)
    网格搜索发现的最佳结果:
    {‘learning_rate’: 0.1}
  • step 6:调节n_estimators的棵数
    1
    2
    3
    4
    5
    xgb_param_grid = {'n_estimators':[50,100,200,300,400,500]}
    grid = GridSearchCV(XGBRegressor( learning_rate=0.1,objective='reg:linear',seed=27,max_depth=7,
                                     min_child_weight=1,gamma=0,colsample_bytree=0.8,subsample=0.9),param_grid=xgb_param_grid, cv=5)
    grid.fit(X_train, y_train)
    grid.grid_scores_, grid.best_params_, grid.best_score_
    1
    2
    3
    4
    5
    6
    7
    8
    ([mean: 0.69015, std: 0.08067, params: {'n_estimators': 50},
      mean: 0.69456, std: 0.08956, params: {'n_estimators': 100},
      mean: 0.69296, std: 0.09306, params: {'n_estimators': 200},
      mean: 0.69270, std: 0.09327, params: {'n_estimators': 300},
      mean: 0.69269, std: 0.09334, params: {'n_estimators': 400},
      mean: 0.69270, std: 0.09335, params: {'n_estimators': 500}],
     {'n_estimators': 100},
     0.6945571414092301)
    网格搜索发现的最佳结果:
    {‘n_estimators’: 100}
    模型最终的参数为：
    1
    2
    3
    4
    5
    6
    7
    XGBRegressor( learning_rate=0.1,
                   objective='reg:linear',
                   seed=27,max_depth=7,
                   min_child_weight=1,
                   gamma=0,
                   colsample_bytree=0.8,
                   subsample=0.9)
    最终评分：
    1
    2
    3
    4
    5
    6
    xgb3 = XGBRegressor( learning_rate=0.1,objective='reg:linear',seed=27,max_depth=7,
                                     min_child_weight=1,gamma=0,colsample_bytree=0.8,subsample=0.9)
    xgb3.fit(X_train,y_train)
    test_predictions = xgb3.predict(X_test)
    r2 = metrics.r2_score(y_test, test_predictions)
    r2
    1
    0.7133043132603486